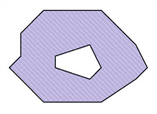
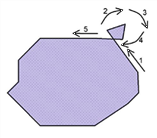
Eine Fläche kann aus mehreren Teilflächen bestehen (mehrteilige Flächen). Generell ist eine mehrteilige Fläche definiert als eine Menge so genannter Teilflächen. Jede Teilfläche ist ein Polygon mit einem Vorzeichen. Dieses ist positiv, wenn die Koordinaten das Polygon entgegen dem Uhrzeigersinn beschreiben und negativ, wenn die Koordinaten mit dem Uhrzeigersinn angeordnet sind. Also werden positive Teilflächen linksherum (also gegen den Uhrzeigersinn) digitalisiert, negative Teilflächen rechtsherum. So wird beim interaktiven Bearbeiten von Polygonen im Netzeditor in eindeutiger Weise ausgedrückt, welche Art von Teilfläche gemeint ist. Diese Orientierung einer Teilfläche ist daher eine wesentliche Objekteigenschaft. Positive Teilflächen sind Teil der Fläche, negative Teilflächen werden subtrahiert (sie werden als Löcher bezeichnet).
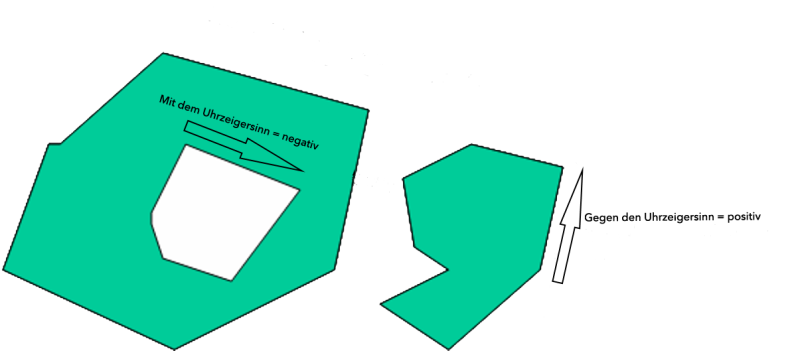
Abbildung 44: Positive und negative Teilflächen
Visum normiert die Definition jeder existierenden Fläche automatisch. Teilflächen können einander nicht schneiden und eine positive Teilfläche wird immer nur negative Teilflächen (direkt) enthalten und umgekehrt.
Was ist eine normalisierte Fläche und warum muss normalisiert werden?
Damit geometrische Operationen (wie zum Beispiel Verschneiden oder die Berechnung von Gebietskennzahlen) auch für komplexe Flächen effizient durchgeführt werden können, muss eine normalisierte Repräsentation verwendet werden. Tabelle 38 zeigt einige Beispiele für die Normalisierung von Flächen.
|
|
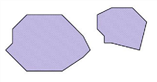
Vorgegebene Fläche |
Normalisierte Form der Fläche |
|
1 |
zwei getrennte Teilflächen |
OK – Fläche bleibt unverändert |
|
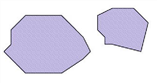
2 |
zwei überlappende Teilflächen |
nicht OK – beide Teilflächen werden vereinigt |
|
3 |
eine Teilfläche mit einem Loch |
OK – Fläche bleibt unverändert |
|
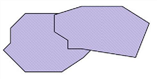
4 |
eine Teilfläche mit einem Loch, welches den Rand der Fläche schneidet |
nicht OK – das Loch entfällt, die Teilfläche wird angepasst |
|
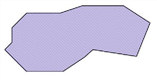
5 |
eine Teilfläche, deren Rand sich selbst schneidet |
nicht OK – das negativ umlaufende Stück wird entfernt |
Tabelle 38: Beispiele für die Normalisierung von Flächen
Eine Fläche ist somit normalisiert, falls die folgenden Bedingungen erfüllt sind:
- Teilflächen gleicher Orientierung enthalten keine Überlappungen. Das heißt
- alle positiven Teilflächen sind getrennt (Kriterium 1a).
- alle negativen Teilflächen sind untereinander getrennt sind und berühren die offene Ebene nicht (Kriterium 1b).
- Der Rand jeder Teilfläche schneidet sich nicht selbst (Kriterium 2).
Um zu verstehen, warum eine normalisierte Repräsentation geometrische Rechenverfahren vereinfacht, genügt das einfache Beispiel der Flächeninhaltsberechnung. Bei normalisierten Flächen kann der Inhalt der Gesamtfläche direkt als Summe der Flächeninhalte ihrer Teilflächen errechnet werden. Das Vorzeichen hängt dabei unmittelbar von der Orientierung ab. Ohne Normalisierung müssten die Inhalte aller auftretenden Schnittmengen vom Ergebnis abgezogen werden. Dies würde einen signifikanten Anstieg der Rechenzeit bedeuten. Die Rechenzeit steigt vor allem deshalb, weil die bloße Bestimmung der Schnittmengen bei Mehrfachüberlappungen ein algorithmisch komplexer Vorgang ist.
Wann wird normalisiert?
Die normalisierte Form von Flächen ist Voraussetzung für eine effiziente Verarbeitung von Polygonen in diversen geometrischen Rechenoperationen. Daher wird diese Eigenschaft beim interaktiven Bearbeiten von Polygonen automatisch sichergestellt. Die oben gezeigten Beispiele können interaktiv zunächst genauso eingefügt werden, wie sie in der linken Spalte dargestellt sind. Beim Beenden des Einfügens führt Visum jedoch automatisch die Normalisierung durch. Auch beim Einlesen von Flächen aus Netzdateien oder Shapefiles kann diese Eigenschaft geprüft und gegebenenfalls durch Umwandlung der Eingabedaten hergestellt werden. Falls die Polygone bereits normalisiert vorliegen oder die Daten nicht für geometrische Rechenoperationen benötigt werden (zum Beispiel bei POI-Layern, die lediglich als Hintergrund dienen), kann dabei jedoch optional auf die Prüfung und Herstellung der normalisierten Form verzichtet und so der Zeitaufwand für den Import reduziert werden.
|
Hinweis: Werden Flächen, die nur für eine Hintergrunddarstellung gedacht sind und daher beim Import nicht normalisiert wurden, zu einem späteren Zeitpunkt doch für Rechenoperationen benötigt, beispielsweise für das Verschneiden, kann es zu fehlerhaften Ergebnissen kommen, weil der normalisierte Zustand Voraussetzung für solche Operationen ist. Wenn Sie nicht sicher sind, in welchem Zustand sich Flächen befinden, können Sie die Flächen vorher explizit normalisieren (Anwendung: Alle Flächen normalisieren). |
Wie genau wird normalisiert (für Experten)?
Beim Normalisieren kommt es auf die Reihenfolge an, in der die Teilflächen einer Fläche definiert werden. Diese Reihenfolge ist zum Beispiel in der Netzdatei durch die Tabelle Flächenelemente definiert.
Eine Vorbehandlung des Teilflächenpolygons ist erforderlich, falls sich sein Rand selbst schneidet (siehe Tabelle 38, Beispiel 5). In diesem Fall wird die Teilfläche in schnittfreie Segmente zerlegt. Die Zerlegung erfolgt so, dass sich sämtliche Komponenten auch gegenseitig nicht schneiden. Die Orientierung der Segmente bleibt erhalten, das heißt ein Schnörkel wie in Tabelle 38, Beispiel 5 wird als negative Teilfläche aufgefasst. Die so ermittelten positiven und negativen Polygone werden mit dem Zwischenergebnis der zuvor betrachteten Teilflächen vereinigt. Bei schnittfreiem Rand ist keine Zerlegung erforderlich. Das vorgegebene Polygon kann direkt mit dem Zwischenergebnis der zuvor betrachteten Teilflächen vereinigt werden.
Bei dieser Vereinigungsoperation kann es vorkommen, dass Teilflächen in einfacher Form verschmolzen werden müssen. In Tabelle 38, Beispiel 2, geschieht dies für zwei positive Teilflächen. Es kann aber auch der Fall auftreten, dass Teilflächen ganz entfallen und andere Teilflächen ihre Form verändern. Dies ist etwa in Tabelle 38, Beispiel 4 der Fall.
Diese Vorgehensweise impliziert insbesondere, dass die erste Teilfläche keine negative Orientierung haben darf. In diesem Fall greift sofort Kriterium 1b, das heißt die Teilfläche wird verworfen.
Besondere Beachtung muss der Frage geschenkt werden, ob die Orientierung eines Teilflächenpolygons zum Enklave-Attribut ihres Flächenelement-Eintrags passt. Beim Netzlesen können hier widersprüchliche Angaben vorliegen. In diesem Fall gewinnt die Enklave-Eigenschaft, das heißt die Orientierung des Polygons wird gegebenenfalls umgekehrt. Der Vorteil dieser Regelung ist, dass eine Teilfläche in der Netzdatei durch Veränderung eines einzigen Attributs von einem positiven zu einem negativen Polygon gemacht werden kann oder umgekehrt.